Powder diffraction data reduction

Powder diffraction data reduction#

This notebook will guide you through the data reduction for the powder diffraction experiment that you simulated with McStas yesterday.

The following is a basic outline of what this notebook will cover:

  • Loading the NeXus files that contain the data

  • Inspect/visualize the data contents

  • How to convert the raw event time-of-arrival coordinate to something more useful (\(\lambda\), \(d\), …)

  • Improve the estimate of neutron time-of-flight

  • Save the reduced data to disk, in a state that is ready for analysis/fitting.

import numpy as np
import scipp as sc
import plopp as pp
import utils

Process the run with a Si sample#

Load the NeXus file data#

folder = "../3-mcstas/powder_Si_high_resolution"

sample_si = utils.load_powder(folder)

The first way to inspect the data is to view the HTML representation of the loaded object.

Try to explore what is inside the data, and familiarize yourself with the different sections (Dimensions, Coordinates, Data).

sample_si
Show/Hide data repr Show/Hide attributes
scipp.DataArray (130.58 MB)
    • events: 1426216
    • position
      (events)
      vector3
      m
      [ 1.9190263 -0.2625 157.67299845], [ 1.9190263 -0.1875 157.67299845], ..., [ -3.21576924 -0.4875 159.2183965 ], [ -3.46803064 -0.1875 161.07197826]
      Values:
      array([[  1.9190263 ,  -0.2625    , 157.67299845],
       [  1.9190263 ,  -0.1875    , 157.67299845],
       [  0.97940155,   0.5625    , 157.23982551],
       ...,
       [ -2.78600701,  -0.1875    , 158.48147104],
       [ -3.21576924,  -0.4875    , 159.2183965 ],
       [ -3.46803064,  -0.1875    , 161.07197826]], shape=(1426216, 3))
    • sample_position
      ()
      vector3
      m
      [ 0. 0. 160.6]
      Values:
      array([  0. ,   0. , 160.6])
    • sim_source_time
      (events)
      float64
      s
      0.000, 0.000, ..., 0.002, 0.004
      Values:
      array([0.00020381, 0.00020381, 0.00044506, ..., 0.00224308, 0.00209017,
       0.00364308], shape=(1426216,))
    • sim_speed
      (events)
      float64
      m/s
      1258.527, 1258.527, ..., 2125.108, 3249.229
      Values:
      array([1258.52717597, 1258.52717597, 1223.39680944, ..., 1778.23546527,
       2125.10814501, 3249.22884854], shape=(1426216,))
    • sim_wavelength
      (events)
      float64
      Å
      3.143, 3.143, ..., 1.862, 1.218
      Values:
      array([3.14338386, 3.14338386, 3.23364748, ..., 2.22469639, 1.86156833,
       1.21753013], shape=(1426216,))
    • source_position
      ()
      vector3
      m
      [0. 0. 0.]
      Values:
      array([0., 0., 0.])
    • time_origin
      ()
      float64
      s
      0.0
      Values:
      array(0.)
    • toa
      (events)
      float64
      s
      0.131, 0.131, ..., 0.079, 0.054
      Values:
      array([0.13061412, 0.13061843, 0.13461796, ..., 0.09452714, 0.07936538,
       0.05415352], shape=(1426216,))
    • x
      (events)
      float64
      m
      1.919, 1.919, ..., -3.216, -3.468
      Values:
      array([ 1.9190263 ,  1.9190263 ,  0.97940155, ..., -2.78600701,
       -3.21576924, -3.46803064], shape=(1426216,))
    • y
      (events)
      float64
      m
      -0.263, -0.188, ..., -0.487, -0.188
      Values:
      array([-0.2625, -0.1875,  0.5625, ..., -0.1875, -0.4875, -0.1875],
      shape=(1426216,))
    • z
      (events)
      float64
      m
      157.673, 157.673, ..., 159.218, 161.072
      Values:
      array([157.67299845, 157.67299845, 157.23982551, ..., 158.48147104,
       159.2183965 , 161.07197826], shape=(1426216,))
    • (events)
      float64
      counts
      0.547, 0.547, ..., 7.707e-08, 2.324
      σ = 0.547, 0.547, ..., 7.707e-08, 2.324
      Values:
      array([5.47429129e-01, 5.47429129e-01, 9.16157772e+00, ...,
       1.22053637e-06, 7.70708749e-08, 2.32399977e+00], shape=(1426216,))

      Variances (σ²):
      array([2.99678651e-01, 2.99678651e-01, 8.39345063e+01, ...,
       1.48970904e-12, 5.93991976e-15, 5.40097492e+00], shape=(1426216,))

Visualize the data#

Here is a 2D visualization of the neutron counts, histogrammed along the x and toadimensions:

sample_si.hist(x=200, toa=200).plot(norm="log", vmin=1.0e-2)
../_images/608bafa939d0dc07bbbd2ee2b0ab676a5f033c9c977a9cf923650ac32ff2ec0a.svg

We can also visualize the events in 3D, which show the shape of the detector panels:

pp.scatter3d(sample_si[::20], pos='position', cbar=True, vmin=0.01, pixel_size=0.07)

Coordinate transformations#

The first step of this data reduction workflow is to convert the raw event coordinates (position, time-of-flight) to something physically meaningful such as wavelength (\(\lambda\)) or d-spacing (\(d\)).

Scipp has a dedicated method for this called transform_coords (see docs here).

We begin with a standard graph which describes how to compute e.g. the wavelength from the other coordinates in the raw data.

from scippneutron.conversion.graph.beamline import beamline
from scippneutron.conversion.graph.tof import kinematic

graph = {**beamline(scatter=True), **kinematic("tof")}

def compute_tof(toa, time_origin):
    return toa - time_origin

graph['tof'] = compute_tof
sc.show_graph(graph, simplified=True)
../_images/382e195bec02074da58500a05e822c21992a79ebf55211623c388366ed97c814.svg

To compute the wavelength of all the events, we simply call transform_coords on our loaded data, requesting the name of the coordinate we want in the output ("wavelength"), as well as providing it the graph to be used to compute it (i.e. the one we defined just above).

This yields

si_wav = sample_si.transform_coords(["wavelength", "two_theta"], graph=graph)
si_wav
Show/Hide data repr Show/Hide attributes
scipp.DataArray (217.63 MB)
    • events: 1426216
    • L1
      ()
      float64
      m
      160.6
      Values:
      array(160.6)
    • L2
      (events)
      float64
      m
      3.510, 3.505, ..., 3.534, 3.505
      Values:
      array([3.50982995, 3.50501872, 3.54491273, ..., 3.50501872, 3.5337878 ,
       3.50501872], shape=(1426216,))
    • Ltotal
      (events)
      float64
      m
      164.110, 164.105, ..., 164.134, 164.105
      Values:
      array([164.10982995, 164.10501872, 164.14491273, ..., 164.10501872,
       164.1337878 , 164.10501872], shape=(1426216,))
    • incident_beam
      ()
      vector3
      m
      [ 0. 0. 160.6]
      Values:
      array([  0. ,   0. , 160.6])
    • position
      (events)
      vector3
      m
      [ 1.9190263 -0.2625 157.67299845], [ 1.9190263 -0.1875 157.67299845], ..., [ -3.21576924 -0.4875 159.2183965 ], [ -3.46803064 -0.1875 161.07197826]
      Values:
      array([[  1.9190263 ,  -0.2625    , 157.67299845],
       [  1.9190263 ,  -0.1875    , 157.67299845],
       [  0.97940155,   0.5625    , 157.23982551],
       ...,
       [ -2.78600701,  -0.1875    , 158.48147104],
       [ -3.21576924,  -0.4875    , 159.2183965 ],
       [ -3.46803064,  -0.1875    , 161.07197826]], shape=(1426216, 3))
    • sample_position
      ()
      vector3
      m
      [ 0. 0. 160.6]
      Values:
      array([  0. ,   0. , 160.6])
    • scattered_beam
      (events)
      vector3
      m
      [ 1.9190263 -0.2625 -2.92700155], [ 1.9190263 -0.1875 -2.92700155], ..., [-3.21576924 -0.4875 -1.3816035 ], [-3.46803064 -0.1875 0.47197826]
      Values:
      array([[ 1.9190263 , -0.2625    , -2.92700155],
       [ 1.9190263 , -0.1875    , -2.92700155],
       [ 0.97940155,  0.5625    , -3.36017449],
       ...,
       [-2.78600701, -0.1875    , -2.11852896],
       [-3.21576924, -0.4875    , -1.3816035 ],
       [-3.46803064, -0.1875    ,  0.47197826]], shape=(1426216, 3))
    • sim_source_time
      (events)
      float64
      s
      0.000, 0.000, ..., 0.002, 0.004
      Values:
      array([0.00020381, 0.00020381, 0.00044506, ..., 0.00224308, 0.00209017,
       0.00364308], shape=(1426216,))
    • sim_speed
      (events)
      float64
      m/s
      1258.527, 1258.527, ..., 2125.108, 3249.229
      Values:
      array([1258.52717597, 1258.52717597, 1223.39680944, ..., 1778.23546527,
       2125.10814501, 3249.22884854], shape=(1426216,))
    • sim_wavelength
      (events)
      float64
      Å
      3.143, 3.143, ..., 1.862, 1.218
      Values:
      array([3.14338386, 3.14338386, 3.23364748, ..., 2.22469639, 1.86156833,
       1.21753013], shape=(1426216,))
    • source_position
      ()
      vector3
      m
      [0. 0. 0.]
      Values:
      array([0., 0., 0.])
    • time_origin
      ()
      float64
      s
      0.0
      Values:
      array(0.)
    • toa
      (events)
      float64
      s
      0.131, 0.131, ..., 0.079, 0.054
      Values:
      array([0.13061412, 0.13061843, 0.13461796, ..., 0.09452714, 0.07936538,
       0.05415352], shape=(1426216,))
    • tof
      (events)
      float64
      s
      0.131, 0.131, ..., 0.079, 0.054
      Values:
      array([0.13061412, 0.13061843, 0.13461796, ..., 0.09452714, 0.07936538,
       0.05415352], shape=(1426216,))
    • two_theta
      (events)
      float64
      rad
      2.557, 2.559, ..., 1.972, 1.436
      Values:
      array([2.55701273, 2.55909034, 2.81733147, ..., 2.21984311, 1.9724811 ,
       1.43572818], shape=(1426216,))
    • wavelength
      (events)
      float64
      Å
      3.149, 3.149, ..., 1.913, 1.305
      Values:
      array([3.14858595, 3.1487821 , 3.24440896, ..., 2.27873933, 1.91290385,
       1.30546381], shape=(1426216,))
    • x
      (events)
      float64
      m
      1.919, 1.919, ..., -3.216, -3.468
      Values:
      array([ 1.9190263 ,  1.9190263 ,  0.97940155, ..., -2.78600701,
       -3.21576924, -3.46803064], shape=(1426216,))
    • y
      (events)
      float64
      m
      -0.263, -0.188, ..., -0.487, -0.188
      Values:
      array([-0.2625, -0.1875,  0.5625, ..., -0.1875, -0.4875, -0.1875],
      shape=(1426216,))
    • z
      (events)
      float64
      m
      157.673, 157.673, ..., 159.218, 161.072
      Values:
      array([157.67299845, 157.67299845, 157.23982551, ..., 158.48147104,
       159.2183965 , 161.07197826], shape=(1426216,))
    • (events)
      float64
      counts
      0.547, 0.547, ..., 7.707e-08, 2.324
      σ = 0.547, 0.547, ..., 7.707e-08, 2.324
      Values:
      array([5.47429129e-01, 5.47429129e-01, 9.16157772e+00, ...,
       1.22053637e-06, 7.70708749e-08, 2.32399977e+00], shape=(1426216,))

      Variances (σ²):
      array([2.99678651e-01, 2.99678651e-01, 8.39345063e+01, ...,
       1.48970904e-12, 5.93991976e-15, 5.40097492e+00], shape=(1426216,))

The result has a wavelength coordinate. We can also plot the result:

si_wav.hist(two_theta=128, wavelength=200).plot(norm='log', vmin=1.0e-3)
../_images/9e3496dae7db9c194aa6ab83c3fc0cb955efc2f9c793a0079bae1a34ff630472.svg

Exercise 1: convert raw data to d-spacing#

Instead of wavelength as in the example above, the task is now to convert the raw data to interplanar lattice spacing \(d\).

The transformation graph is missing the computation for \(d\) so you will have to add it in yourself. As a reminder, \(d\) is computed as follows

\[d = \frac{\lambda}{2 \sin \theta}\]

You have to:

  • create a function that computes \(d\)

  • add it to the graph with name “dspacing”

  • call transform_coords using the new graph

Note that the graph already contains the necessary components to compute the scattering angle \(2 \theta\) (called two_theta in code).

Solution:

Hide code cell content 
def compute_d(two_theta, wavelength):
    return wavelength / (2 * sc.sin(two_theta / 2))


graph["dspacing"] = compute_d

# Show the updated graph
display(sc.show_graph(graph, simplified=True))

# Run the coordinate transformation
si_dspacing = sample_si.transform_coords("dspacing", graph=graph)
si_dspacing
../_images/a53326bf16400a63a211bc3d95026dd72b86f0da006ca3509057acb611b93324.svg
Show/Hide data repr Show/Hide attributes
scipp.DataArray (228.51 MB)
    • events: 1426216
    • L1
      ()
      float64
      m
      160.6
      Values:
      array(160.6)
    • L2
      (events)
      float64
      m
      3.510, 3.505, ..., 3.534, 3.505
      Values:
      array([3.50982995, 3.50501872, 3.54491273, ..., 3.50501872, 3.5337878 ,
       3.50501872], shape=(1426216,))
    • Ltotal
      (events)
      float64
      m
      164.110, 164.105, ..., 164.134, 164.105
      Values:
      array([164.10982995, 164.10501872, 164.14491273, ..., 164.10501872,
       164.1337878 , 164.10501872], shape=(1426216,))
    • dspacing
      (events)
      float64
      Å
      1.644, 1.644, ..., 1.147, 0.992
      Values:
      array([1.64402161, 1.64361115, 1.64376142, ..., 1.27209525, 1.14688356,
       0.99232951], shape=(1426216,))
    • incident_beam
      ()
      vector3
      m
      [ 0. 0. 160.6]
      Values:
      array([  0. ,   0. , 160.6])
    • position
      (events)
      vector3
      m
      [ 1.9190263 -0.2625 157.67299845], [ 1.9190263 -0.1875 157.67299845], ..., [ -3.21576924 -0.4875 159.2183965 ], [ -3.46803064 -0.1875 161.07197826]
      Values:
      array([[  1.9190263 ,  -0.2625    , 157.67299845],
       [  1.9190263 ,  -0.1875    , 157.67299845],
       [  0.97940155,   0.5625    , 157.23982551],
       ...,
       [ -2.78600701,  -0.1875    , 158.48147104],
       [ -3.21576924,  -0.4875    , 159.2183965 ],
       [ -3.46803064,  -0.1875    , 161.07197826]], shape=(1426216, 3))
    • sample_position
      ()
      vector3
      m
      [ 0. 0. 160.6]
      Values:
      array([  0. ,   0. , 160.6])
    • scattered_beam
      (events)
      vector3
      m
      [ 1.9190263 -0.2625 -2.92700155], [ 1.9190263 -0.1875 -2.92700155], ..., [-3.21576924 -0.4875 -1.3816035 ], [-3.46803064 -0.1875 0.47197826]
      Values:
      array([[ 1.9190263 , -0.2625    , -2.92700155],
       [ 1.9190263 , -0.1875    , -2.92700155],
       [ 0.97940155,  0.5625    , -3.36017449],
       ...,
       [-2.78600701, -0.1875    , -2.11852896],
       [-3.21576924, -0.4875    , -1.3816035 ],
       [-3.46803064, -0.1875    ,  0.47197826]], shape=(1426216, 3))
    • sim_source_time
      (events)
      float64
      s
      0.000, 0.000, ..., 0.002, 0.004
      Values:
      array([0.00020381, 0.00020381, 0.00044506, ..., 0.00224308, 0.00209017,
       0.00364308], shape=(1426216,))
    • sim_speed
      (events)
      float64
      m/s
      1258.527, 1258.527, ..., 2125.108, 3249.229
      Values:
      array([1258.52717597, 1258.52717597, 1223.39680944, ..., 1778.23546527,
       2125.10814501, 3249.22884854], shape=(1426216,))
    • sim_wavelength
      (events)
      float64
      Å
      3.143, 3.143, ..., 1.862, 1.218
      Values:
      array([3.14338386, 3.14338386, 3.23364748, ..., 2.22469639, 1.86156833,
       1.21753013], shape=(1426216,))
    • source_position
      ()
      vector3
      m
      [0. 0. 0.]
      Values:
      array([0., 0., 0.])
    • time_origin
      ()
      float64
      s
      0.0
      Values:
      array(0.)
    • toa
      (events)
      float64
      s
      0.131, 0.131, ..., 0.079, 0.054
      Values:
      array([0.13061412, 0.13061843, 0.13461796, ..., 0.09452714, 0.07936538,
       0.05415352], shape=(1426216,))
    • tof
      (events)
      float64
      s
      0.131, 0.131, ..., 0.079, 0.054
      Values:
      array([0.13061412, 0.13061843, 0.13461796, ..., 0.09452714, 0.07936538,
       0.05415352], shape=(1426216,))
    • two_theta
      (events)
      float64
      rad
      2.557, 2.559, ..., 1.972, 1.436
      Values:
      array([2.55701273, 2.55909034, 2.81733147, ..., 2.21984311, 1.9724811 ,
       1.43572818], shape=(1426216,))
    • wavelength
      (events)
      float64
      Å
      3.149, 3.149, ..., 1.913, 1.305
      Values:
      array([3.14858595, 3.1487821 , 3.24440896, ..., 2.27873933, 1.91290385,
       1.30546381], shape=(1426216,))
    • x
      (events)
      float64
      m
      1.919, 1.919, ..., -3.216, -3.468
      Values:
      array([ 1.9190263 ,  1.9190263 ,  0.97940155, ..., -2.78600701,
       -3.21576924, -3.46803064], shape=(1426216,))
    • y
      (events)
      float64
      m
      -0.263, -0.188, ..., -0.487, -0.188
      Values:
      array([-0.2625, -0.1875,  0.5625, ..., -0.1875, -0.4875, -0.1875],
      shape=(1426216,))
    • z
      (events)
      float64
      m
      157.673, 157.673, ..., 159.218, 161.072
      Values:
      array([157.67299845, 157.67299845, 157.23982551, ..., 158.48147104,
       159.2183965 , 161.07197826], shape=(1426216,))
    • (events)
      float64
      counts
      0.547, 0.547, ..., 7.707e-08, 2.324
      σ = 0.547, 0.547, ..., 7.707e-08, 2.324
      Values:
      array([5.47429129e-01, 5.47429129e-01, 9.16157772e+00, ...,
       1.22053637e-06, 7.70708749e-08, 2.32399977e+00], shape=(1426216,))

      Variances (σ²):
      array([2.99678651e-01, 2.99678651e-01, 8.39345063e+01, ...,
       1.48970904e-12, 5.93991976e-15, 5.40097492e+00], shape=(1426216,))

Histogram the data in d-spacing#

The final step in processing the sample run is to histogram the data into \(d\) bins.

dbins = sc.linspace ('dspacing', 0.5, 2.5, 2001, unit='angstrom')
ntheta = 128

si_dspacing_hist = si_dspacing.hist(two_theta=ntheta, dspacing=dbins)
si_dspacing_hist.plot(norm='log', vmin=1.0e-3)
../_images/b796cb94e15c2b2afad60fe82b6ff6aafeefc2d40f1d2936a9afdee765a9dc7d.svg 
si_dspacing_hist.sum('two_theta').plot()
../_images/7bb353c7c2f9f8579dbb99ee20a937e8867257222b1c6fb09b64b1f1bbf880ee.svg

Exercise 2: Correct the time-of-flight#

Time-of-flight at a long-pulsed source#

The time-of-flight of a neutron is typically not known from experimental measurements. The only two parameters that we are able to record are usually the time at which the pulse was emitted (named time_origin in our dataset), and the timestamp when a neutron was detected by a detector pixel (named toa, standing for time-of-arrival).

The difference between these two times is commonly used to compute an approximate time-of-flight. This approximation performs well at neutron sources with a short pulse, where it is satisfactory to assume that all neutrons left the source at the same time.

At a long-pulsed source (lasting a few milliseconds) such as ESS, with high-precision instruments, this approximation is no longer valid.

This is in fact the reason why in the \(2\theta\) vs d-spacing plot, the bright lines appear curved while they should in reality be vertical.

In the following exercise, we will add a correction to our time-of-flight computation to improve our results.

Finding a new time-distance origin#

One way to look at the problem is to visualize the paths of each neutron that made it to the detector, on a time-distance diagram.

The neutrons begin at the source (bottom left), travel along the guide, go through the chopper, and finally arrive at the detectors (top).

from powder_utils import time_distance_diagram

time_distance_diagram(si_wav)
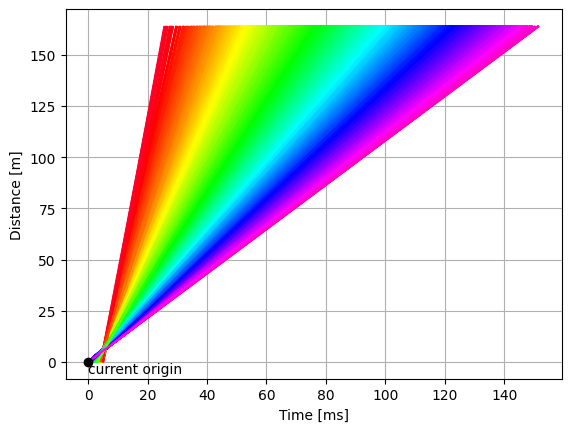
../_images/25c92eb56a0ab96bf1358cd5b2f45f1566828b4f6827597e78eef4236ac992a6.png

As the figure above illustrates, the current time-of-flight computation (tof = toa - time_origin) assumes that all neutrons were born at \(t = 0\) (black dot).

This is clearly not the case from looking at the neutron tracks.

Exercise: find a new origin#

  • Inspect the time-distance diagram and try to find a point which would be a better representation of a common origin for all tracks.

  • Set the origin as coordinates on the original data (hint: you will need to update the source_position and time_origin coordinates).

  • Compute wavelength/d-spacing again.

Solution:

Hide code cell content 
better = sample_si.copy(deep=False)

# Read off the plot that the lines cross as they go through the chopper:
# time=5.53, distance=6.5 (approximately)
better.coords['source_position'] = sc.vector([0, 0, 6.5], unit='m')
better.coords['time_origin'] = sc.scalar(5.53, unit='ms').to(unit='s')

better_dspacing = better.transform_coords("dspacing", graph=graph)
better_dspacing
Show/Hide data repr Show/Hide attributes
scipp.DataArray (228.51 MB)
    • events: 1426216
    • L1
      ()
      float64
      m
      154.1
      Values:
      array(154.1)
    • L2
      (events)
      float64
      m
      3.510, 3.505, ..., 3.534, 3.505
      Values:
      array([3.50982995, 3.50501872, 3.54491273, ..., 3.50501872, 3.5337878 ,
       3.50501872], shape=(1426216,))
    • Ltotal
      (events)
      float64
      m
      157.610, 157.605, ..., 157.634, 157.605
      Values:
      array([157.60982995, 157.60501872, 157.64491273, ..., 157.60501872,
       157.6337878 , 157.60501872], shape=(1426216,))
    • dspacing
      (events)
      float64
      Å
      1.639, 1.639, ..., 1.111, 0.928
      Values:
      array([1.63934691, 1.63894199, 1.64122825, ..., 1.24707043, 1.11096768,
       0.92774245], shape=(1426216,))
    • incident_beam
      ()
      vector3
      m
      [ 0. 0. 154.1]
      Values:
      array([  0. ,   0. , 154.1])
    • position
      (events)
      vector3
      m
      [ 1.9190263 -0.2625 157.67299845], [ 1.9190263 -0.1875 157.67299845], ..., [ -3.21576924 -0.4875 159.2183965 ], [ -3.46803064 -0.1875 161.07197826]
      Values:
      array([[  1.9190263 ,  -0.2625    , 157.67299845],
       [  1.9190263 ,  -0.1875    , 157.67299845],
       [  0.97940155,   0.5625    , 157.23982551],
       ...,
       [ -2.78600701,  -0.1875    , 158.48147104],
       [ -3.21576924,  -0.4875    , 159.2183965 ],
       [ -3.46803064,  -0.1875    , 161.07197826]], shape=(1426216, 3))
    • sample_position
      ()
      vector3
      m
      [ 0. 0. 160.6]
      Values:
      array([  0. ,   0. , 160.6])
    • scattered_beam
      (events)
      vector3
      m
      [ 1.9190263 -0.2625 -2.92700155], [ 1.9190263 -0.1875 -2.92700155], ..., [-3.21576924 -0.4875 -1.3816035 ], [-3.46803064 -0.1875 0.47197826]
      Values:
      array([[ 1.9190263 , -0.2625    , -2.92700155],
       [ 1.9190263 , -0.1875    , -2.92700155],
       [ 0.97940155,  0.5625    , -3.36017449],
       ...,
       [-2.78600701, -0.1875    , -2.11852896],
       [-3.21576924, -0.4875    , -1.3816035 ],
       [-3.46803064, -0.1875    ,  0.47197826]], shape=(1426216, 3))
    • sim_source_time
      (events)
      float64
      s
      0.000, 0.000, ..., 0.002, 0.004
      Values:
      array([0.00020381, 0.00020381, 0.00044506, ..., 0.00224308, 0.00209017,
       0.00364308], shape=(1426216,))
    • sim_speed
      (events)
      float64
      m/s
      1258.527, 1258.527, ..., 2125.108, 3249.229
      Values:
      array([1258.52717597, 1258.52717597, 1223.39680944, ..., 1778.23546527,
       2125.10814501, 3249.22884854], shape=(1426216,))
    • sim_wavelength
      (events)
      float64
      Å
      3.143, 3.143, ..., 1.862, 1.218
      Values:
      array([3.14338386, 3.14338386, 3.23364748, ..., 2.22469639, 1.86156833,
       1.21753013], shape=(1426216,))
    • source_position
      ()
      vector3
      m
      [0. 0. 6.5]
      Values:
      array([0. , 0. , 6.5])
    • time_origin
      ()
      float64
      s
      0.00553
      Values:
      array(0.00553)
    • toa
      (events)
      float64
      s
      0.131, 0.131, ..., 0.079, 0.054
      Values:
      array([0.13061412, 0.13061843, 0.13461796, ..., 0.09452714, 0.07936538,
       0.05415352], shape=(1426216,))
    • tof
      (events)
      float64
      s
      0.125, 0.125, ..., 0.074, 0.049
      Values:
      array([0.12508412, 0.12508843, 0.12908796, ..., 0.08899714, 0.07383538,
       0.04862352], shape=(1426216,))
    • two_theta
      (events)
      float64
      rad
      2.557, 2.559, ..., 1.972, 1.436
      Values:
      array([2.55701273, 2.55909034, 2.81733147, ..., 2.21984311, 1.9724811 ,
       1.43572818], shape=(1426216,))
    • wavelength
      (events)
      float64
      Å
      3.140, 3.140, ..., 1.853, 1.220
      Values:
      array([3.13963308, 3.13983705, 3.23940905, ..., 2.23391168, 1.85299922,
       1.220496  ], shape=(1426216,))
    • x
      (events)
      float64
      m
      1.919, 1.919, ..., -3.216, -3.468
      Values:
      array([ 1.9190263 ,  1.9190263 ,  0.97940155, ..., -2.78600701,
       -3.21576924, -3.46803064], shape=(1426216,))
    • y
      (events)
      float64
      m
      -0.263, -0.188, ..., -0.487, -0.188
      Values:
      array([-0.2625, -0.1875,  0.5625, ..., -0.1875, -0.4875, -0.1875],
      shape=(1426216,))
    • z
      (events)
      float64
      m
      157.673, 157.673, ..., 159.218, 161.072
      Values:
      array([157.67299845, 157.67299845, 157.23982551, ..., 158.48147104,
       159.2183965 , 161.07197826], shape=(1426216,))
    • (events)
      float64
      counts
      0.547, 0.547, ..., 7.707e-08, 2.324
      σ = 0.547, 0.547, ..., 7.707e-08, 2.324
      Values:
      array([5.47429129e-01, 5.47429129e-01, 9.16157772e+00, ...,
       1.22053637e-06, 7.70708749e-08, 2.32399977e+00], shape=(1426216,))

      Variances (σ²):
      array([2.99678651e-01, 2.99678651e-01, 8.39345063e+01, ...,
       1.48970904e-12, 5.93991976e-15, 5.40097492e+00], shape=(1426216,))
better_dspacing.hist(two_theta=ntheta, dspacing=dbins).plot(norm='log', vmin=1.0e-3)
../_images/b67d99afec745fb2fd6de7e64cf535fb0134731920f85bd7fe2404df673e8bf7.svg 
pp.plot({'original': si_dspacing_hist.sum('two_theta'),
         'improved': better_dspacing.hist(two_theta=ntheta, dspacing=dbins).sum('two_theta')})
../_images/f7667a47dc14613fe83e8142ed2ba34d31210e807c78be5792735911821af7ef.svg

Process the Vanadium run#

folder = "../3-mcstas/powder_vanadium"

sample_van = utils.load_powder(folder)

# Read off the plot that the lines cross as they go through the chopper:
# time=5.53, distance=6.5 (approximately)
sample_van.coords['source_position'] = sc.vector([0, 0, 6.5], unit='m')
sample_van.coords['time_origin'] = sc.scalar(5.53, unit='ms').to(unit='s')

van_dspacing = sample_van.transform_coords("dspacing", graph=graph)
van_dspacing.hist(two_theta=ntheta, dspacing=dbins).plot(norm='log', vmin=1.0e-3)
../_images/62962f8bd697d0cb6081a07626b67f8c08f4c0c1f00c55bb236eab3d4d6b6a35.svg

Normalize by Vanadium#

num = better_dspacing.hist(two_theta=ntheta, dspacing=dbins)
den = van_dspacing.hist(two_theta=num.coords['two_theta'], dspacing=dbins)

# Smooth the Vanadium run 
from scipp.scipy.ndimage import gaussian_filter

smooth_vana = gaussian_filter(
    sc.values(den.sum('two_theta')),
    sigma=sc.scalar(0.02, unit='angstrom')
)

pp.plot({'orig': den.sum('two_theta'), 
         'smooth': smooth_vana}, 
        title='Vanadium - smoothed')
../_images/098be3c2aa4b00a1e4534d0892cce722969637af7fea95a1297ae646cb5c50c3.svg 
normed = (num.sum('two_theta') / smooth_vana)

normed.plot()
../_images/55c093985d850c69caee6d4451d6c7a07b3dcd480372d96a0a31f4fbda957c30.svg

Save to disk#

average_l = better_dspacing.coords["Ltotal"].mean()
average_two_theta = better_dspacing.coords["two_theta"].mean()
difc = sc.to_unit(
    2
    * sc.constants.m_n
    / sc.constants.h
    * average_l
    * sc.sin(0.5 * average_two_theta),
    unit='us / angstrom',
)

average_l , sc.to_unit(average_two_theta, 'deg'), difc

(<scipp.Variable> ()    float64              [m]  157.626,
 <scipp.Variable> ()    float64            [deg]  100.719,
 <scipp.Variable> ()    float64         [10N/mW]  61365.3)

from scippneutron.io import save_xye

result_si = normed.copy(deep=False)
result_si.coords["tof"] = (sc.midpoints(result_si.coords["dspacing"]) * difc).to(unit='us')

save_xye("powder_reduced_Si.xye", result_si.rename_dims(dspacing='tof'),
         header=f"DIFC = {difc.to(unit='us/angstrom').value} [µ/Å] L = {average_l.value} [m] two_theta = {sc.to_unit(average_two_theta, 'deg').value} [deg]\ntof [µs]               Y [counts]               E [counts]")

Process and normalize unknown sample#

folder = "../3-mcstas/powder_sample_2"

unknown = utils.load_powder(folder)

# Read off the plot that the lines cross as they go through the chopper:
# time=5.53, distance=6.5 (approximately)
unknown.coords['source_position'] = sc.vector([0, 0, 6.5], unit='m')
unknown.coords['time_origin'] = sc.scalar(5.53, unit='ms').to(unit='s')

unknown_dspacing = unknown.transform_coords("dspacing", graph=graph)
unknown_dspacing.hist(two_theta=ntheta, dspacing=dbins).plot(norm='log', vmin=1.0e-3)

# Normalize
unknown_num = unknown_dspacing.hist(two_theta=den.coords['two_theta'], dspacing=dbins)

unknown_normed = (unknown_num.sum('two_theta') / smooth_vana)

unknown_normed.plot()
../_images/679b0c066e8acafe9e67c8fdf8a7523bcdc032ecd2ec0c58ea3cafc44483ca79.svg 
average_l = unknown_dspacing.coords["Ltotal"].mean()
average_two_theta = unknown_dspacing.coords["two_theta"].mean()
difc = sc.to_unit(
    2
    * sc.constants.m_n
    / sc.constants.h
    * average_l
    * sc.sin(0.5 * average_two_theta),
    unit='us / angstrom',
)
average_l , sc.to_unit(average_two_theta, 'deg'), difc

(<scipp.Variable> ()    float64              [m]  157.626,
 <scipp.Variable> ()    float64            [deg]  94.7832,
 <scipp.Variable> ()    float64         [10N/mW]  58650.9)

Save to disk#

result_unknown = unknown_normed.copy(deep=False)
result_unknown.coords["tof"] = (sc.midpoints(result_unknown.coords["dspacing"]) * difc).to(unit='us')

save_xye("powder_reduced_unknown.xye", result_unknown.rename_dims(dspacing='tof'),
         header=f"DIFC = {difc.to(unit='us/angstrom').value} [µ/Å] L = {average_l.value} [m] two_theta = {sc.to_unit(average_two_theta, 'deg').value} [deg]\ntof [µs]               Y [counts]               E [counts]")
Contents